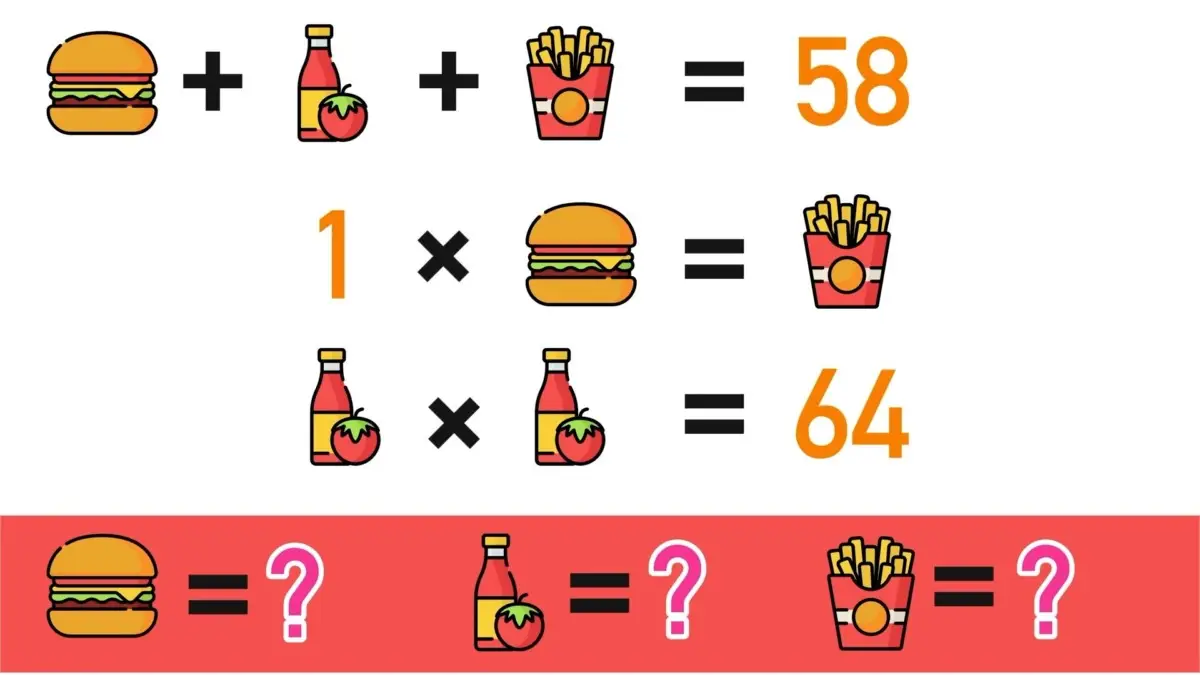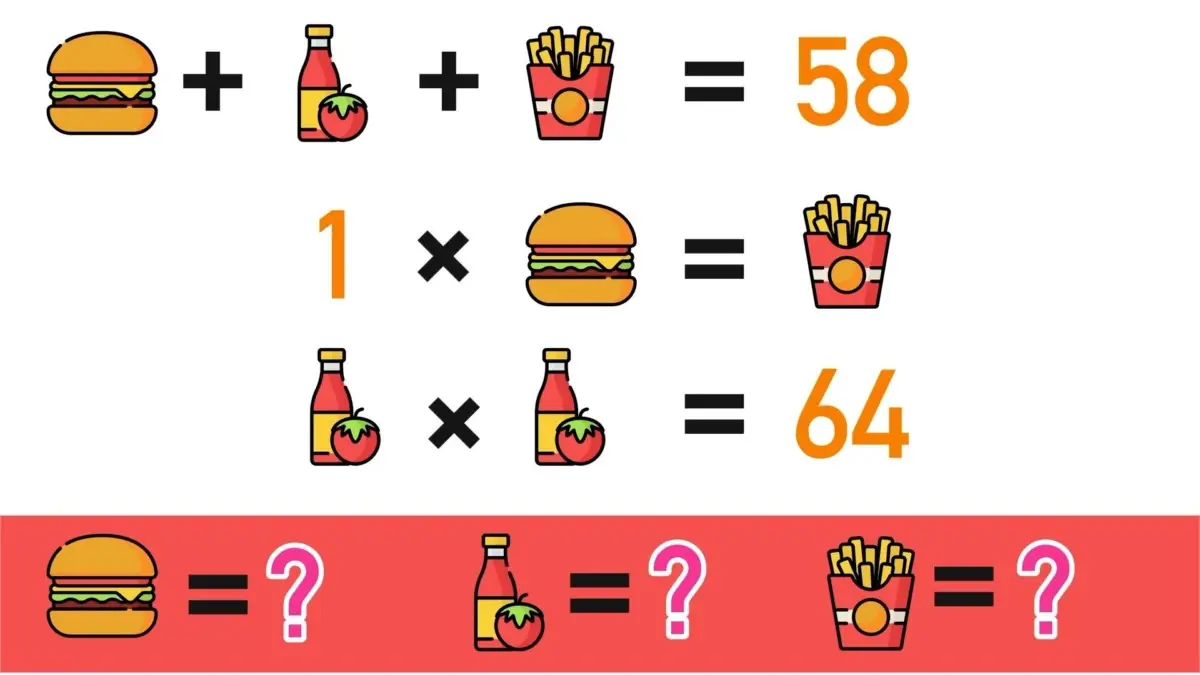Ah, la matematica! Tanto odiata da qualcuno ma tanto amata da qualcun altro. Quando si parla di matematica potremmo immaginare due fazioni studentesche: quella di cui fanno parte gli amanti della materia e quelli, al contrario, che proprio non la sopportano. Solitamente non ci sono grandi vie di mezzo, o la si ama o la si odia.
A prescindere dai propri gusti personali, la matematica è una delle materie di base del percorso scolastico di ogni studente e ci sono delle ragioni per cui è così! La matematica, infatti, permette di imparare dei concetti che saranno utili, se non fondamentali, per la vita dei futuri adulti !
Pensa se non sapessi svolgere i calcoli a mente, o se non sapessi fare il resto. O, ancora, se non fossi in grado di misurare la lunghezza di un tavolo. Sarebbe un bel pasticcio! E’ proprio grazie alla matematica se hai acquisito queste competenze fondamentali per la vita di tutti i giorni.
Un tuffo nella matematica: le frazioni
Le frazioni sono uno degli argomenti più importanti della matematica, insieme, ad esempio, alle quattro operazioni (addizione, sottrazione, moltiplicazione e divisione). Questi due argomenti, come vedremo, non sono poi così lontani l’uno dall’altro. Al contrario, sono strettamente correlati. L’incastro tra i vari argomenti è una situazione molto comune in matematica.
Scopri, adesso, il concetto di frazione! Per far ciò immagina una gustosa torta appena sfornata. Questa, in matematica, rappresenta un intero (infatti, è intera a tutti gli effetti!). Se decidi di tagliarla in parti uguali, starai operando un “frazionamento”. Le parti uguali che avrai creato, quindi, rappresentano una frazione dell’intero. Interessante, vero?
Le frazioni sono rappresentate graficamente con una linea centrale, chiamata linea di frazione, che presenta al di sopra un numero, il denominatore e, al di sotto, un secondo numero, chiamato denominatore. Il numeratore indica quante parti dell’intero considero, mentre il denominare le parti totali in cui è stato suddiviso l’intero.
Le tipologie di frazioni
Riprendendo il concetto espresso nei paragrafi precedenti, scriviamo alcuni esempi di frazioni. 5/6 significa che l’intero (ovvero la torta dell’esempio precedente) è stata divisa in 6 parti totali (il denominatore) e se ne sono presa 5 (il numeratore). Frazioni di questo tipo sono dette frazioni proprie. Differenti sono le frazioni improprie.
Le frazioni improprie presentano numeratore superiore al denominatore, come, per esempio, 10/8. In questo caso, non solo prenderò tutti gli 8 pezzi in cui è stata suddivisa la torta, ma altri due in più, fino ad ottenerne 10. La tipologia di frazione che, tuttavia, ci interessa maggiormente per la risoluzione dell’esercizio è la seguente.
Sto parlando dei numeri misti, ovvero delle combinazioni tra un numero intero e una frazione. Sembra difficile, vero? Più difficile a dirsi che a farsi, di sicuro. Ecco un esempio pratico: 3 1/2. In questo caso si deve operare , trovando il minimo comune multiplo, per ottenere una frazione unica.
Il calcolo delle frazioni
Quando, nei paragrafi precedenti, ho affermato che le frazioni sono strettamente correlate alle 4 operazioni (addizione, sottrazione, moltiplicazione e divisione), mi riferivo al fatto che è possibile effettuare i calcoli tra più frazioni, utilizzando proprio le 4 operazioni. Le frazioni, infatti, non sono numeri a sé stanti ma con essi si può giocare!
Da qui deriva che 1/2 + 1/2 = 1, ovvero che sommando due metà (“un mezzo più un mezzo”) si ottiene un intero. Se ho metà della torta e le metto vicine, otterrò una torta intera. Come con l’addizione, si possono effettuare calcoli con sottrazione, moltiplicazione e divisione, seguendo delle regole specifiche.
Se abbiamo una situazione simile a quella dell’esercizio proposto, ovvero in cui ci viene detto a quanto valore corrisponde una parte dell’intero, ovvero la frazione corrisponde, per trovare, appunto, l’intero si dovrà moltiplicare il valore della parte per la frazione a cui corrisponde. Se 1/5 (ovvero una parte su 5) di torta corrisponde a 50 grammi, l’intera torta corrisponderà a 5 x 50 = 250 g.
Scopri la soluzione dell’esercizio proposto!
Adesso che sei giunto a questo punto della lettura, avendo rispolverato un po’ di informazioni sul concetto di frazione, avendo letto alcuni esempi pratici e avendo avuto modo di riordinare le idee, non ti resta altro da fare che provare a trovare la soluzione dell’esercizio. Prenditi il tempo che ti occorre.
Una volta che avrai trovato la soluzione, prosegui con la lettura. Immagina la torta dell’esempio precedente, se ho una frazione di 1/3, significa che è stata divisa in tre parti uguali. Dal testo dell’esercizio, si evince che una di queste tre parti vale 4. Per trovare il valore di tutte e tre le parti, basterà fare: 4 x 3 = 12. 12 è la soluzione corretta.